3866. K-ое число

Вы работаете на компанию МакроХард в отделе структуры данных. После неудачного решения предыдущей задаче о вставки ключей, Вас попросили написать новую структуру данных, позволяющую быстро находить k-ую порядковую статистику на указанном отрезке.

Задан массив a[1...n] различных целых чисел. Необходимо отвечать на вопросы Q(i, j, k) следующего вида: "Найти k-ое число на отрезке a[i ... j], если все числа на этом отрезке предварительно отсортировать".

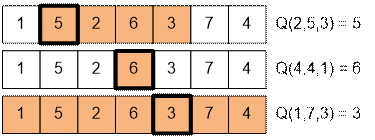
Например, рассмотрим отрезок a = (1, 5, 2, 6, 3, 7, 4). Рассмотрим запрос Q(2, 5, 3). Отрезком a[2 ... 5] будет (5, 2, 6, 3). Отсортировав числа, получим (2, 3, 5, 6). Третьим элементом будет 5. Ответом на запрос будет 5.

Вход. Первая строка содержит размер массива n и количество запросов m (1 ≤ n ≤ 100000, 1 ≤ m ≤ 5000).

Вторая строка содержит n разных целых чисел, не превосходящих 10⁹ по абсолютному значению – массив чисел, к которому будут ставиться запросы.

Следующие m строк содержат запросы, каждый из которых состоит из трех чисел: i, j и k (0 ≤ i ≤ j ≤ n, 0 ≤ k ≤ j – i + 1) и представляет собой запрос Q(i, j, k).

Выход. Для каждого запроса вывести k-ое число в отсортированном отрезке a[i ... j].

Пример входа	Пример выхода
7 3 1 5 2 6 3 7 4 2 5 3 4 4 1 1 7 3	5 6 3

РЕШЕНИЕ

структуры данных – дерево отрезков

Анализ алгоритма

Заведем в каждой вершине дерева отрезков дополнительный массив. Вершина, соответствующая фундаментальному отрезку [i; j], содержит в своем массиве отсортированный набор чисел a_i, …, a_j.

Пусть запрос Query(l, r, x) находит количество чисел из интервала [l, r], которые меньше x. Для этого разобьем этот интервал на множество фундаментальных отрезков, в каждом из которых совершим бинарный поиск, подсчитав число элементов, меньших x. Время запроса составит .

Ответ на запрос Q(i, j, k) будем искать бинарным поиском. Следует найти такое a_p из интервала [a_i, …, a_j], что Query(l, r, a_p) равно k – 1. То есть если a_p является k –ым элементов на отрезке [i; j], то количество чисел на этом отрезке, меньших a_p, равно k – 1. Принципиальным в этой задаче является то, что все входные числа разные. Таким образом запрос выполняется за .

Пример

Рассмотрим выполнение запросов:

Реализация алгоритма

В массив а считываем входные числа.

#define MAX 100010

int a[MAX];

Объявим дерево отрезков SegTree, в каждой вершине которого будет храниться еще один линейный массив.

vector<vector<int> > SegTree;

Построение дерева отрезков. Листы хранят массив из одного элемента.

void build(int Vertex, int LeftPos, int RightPos)

{

if (LeftPos == RightPos)

SegTree[Vertex].push_back(a[LeftPos]);

else

{

int Middle = (LeftPos + RightPos) / 2;

build (2*Vertex, LeftPos, Middle);

build (2*Vertex+1, Middle+1, RightPos);

SegTree[Vertex].resize(RightPos - LeftPos + 1);

В каждой вершине хранится остортированный список элементов, которые она покрывет.

merge(SegTree[2*Vertex].begin(),SegTree[2*Vertex].end(),

SegTree[2*Vertex+1].begin(),SegTree[2*Vertex+1].end(),

SegTree[Vertex].begin());

}

}

Возвращаем количество элементов на промежутке [Left; Right], строго меньших x.

int Query(int Vertex, int LeftPos, int RightPos,

int Left, int Right, int x)

{

if (Left > Right) return 0;

if ((LeftPos == Left) && (RightPos == Right))

Дошли до вершины Vertex, которой соответствует фундаментальный отрезок [LeftPos; RightPos] = [Left; Right]. В ней хранится отсортированный массив чисел. При помощи бинарного поиска ищем в нем количество элементов, меньших x.

return lower_bound(SegTree[Vertex].begin(),SegTree[Vertex].end(),x)

– SegTree[Vertex].begin();

int Middle = (LeftPos + RightPos) / 2;

return Query(2*Vertex, LeftPos, Middle, Left, min(Middle,Right), x)

+ Query(2*Vertex+1, Middle+1, RightPos, max(Left,Middle+1), Right, x);

}

Основная часть программы. Читаем входные данные.

scanf("%d %d",&n,&m);

for(i = 1; i <= n; i++)

scanf("%d",&a[i]);

Строим дерево отрезков.

SegTree.resize(4*n);

build(1,1,n);

Сортируем массив чисел.

sort(a+1,a+n+1);

Обрабатываем m запросов.

while(m--)

{

scanf("%d %d %d",&i,&j,&k);

В отсортированном массиве а ищем бинарным поиском такое число a[mid], что на промежутке [i; j] имеется в точности k – 1 число, меньшее a[mid]. Бинарный поиск продолжаем, пока промежуток поиска [left; right] содержит более одного элемента.

int left = 1, right = n;

while (left < right)

{

int mid = (left + right) / 2;

if (Query(1, 1, n, i, j, a[mid] + 1) < k)

left = mid + 1;

else

right = mid;

}

Выводим ответ.

printf("%d\n", a[left]);

}